1. Major past hobbies
Wikipedia: Click here for highlights & gallery
Between 2005 and 2018 I was a prolific author and editor of Wikipedia articles related to physics, math, and engineering. Here are a couple animations I've made, with much more content at the link:
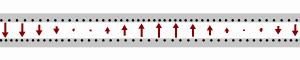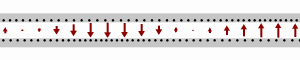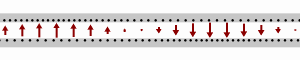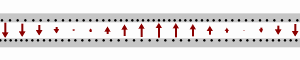
Schematic showing how a wave flows down a transmission line. The black dots represent electrons, and the arrows show the electric field.
A harmonic oscillator in classical mechanics (A-B) and quantum mechanics (C-H). In (A-B), a ball, attached to a spring (gray line), oscillates back and forth. In (C-H), wavefunction solutions to the Time-Dependent Schrödinger Equation are shown for the same potential. The horizontal axis is position, the vertical axis is the real part (blue) or imaginary part (red) of the wavefunction. (C,D,E,F) are stationary states (energy eigenstates), which come from solutions to the Time-Independent Schrödinger Equation. (G-H) are non-stationary states, solutions to the Time-Dependent but not Time-Independent Schrödinger Equation. (G) is a randomly-generated quantum superposition of the four states (C-F). (H) is a “coherent state” (“Glauber state”) which somewhat resembles the classical state B.
Cold fusion blog: Click here
Everyone knows that there's no such thing as cold fusion (a.k.a. "LENR"), but I didn't want to take anyone's word for it, I wanted to check for myself. Thus, I made a hobby out of carefully reading the papers and studying the arguments of cold fusion proponents. After 29 blog posts over 4 years, I concluded that the mainstream consensus is correct! There is indeed no such thing as cold fusion. You can get the summary in my final 3 blog posts: the case against cold fusion experiments, the case against cold fusion theory, and the dangerous dark side of cold fusion research. Meanwhile, the blog was a nice excuse to write lots of fun pedagogical posts about quantum optics, nuclear physics, relativistic quantum mechanics, Bose-Einstein condensation, statistical mechanics, and much more.
Shockley-Queisser limit: Click here for my tutorial slideshow, or click here for calculation code (Python) with discussion
In 1961, William Shockley and Hans-Joachim Queisser famously proved that certain types of solar cells cannot be more than ~35% efficient. Here you can learn how that calculation works in detail, and also how and why various types of solar cells are able to exceed the limit. The Python code includes not only calculation of the efficiency itself, but also harder-to-find related calculations: Plots of the ideal “VOC” and “ISC”, and detailed breakdowns of the losses. I used this program to make some graphs that I uploaded to Wikipedia, and have since seen all around the internet and conferences. (While I was at it, I also wrote up a detailed derivation / explanation of the “ultimate” solar power efficiency limit, which is higher than the Shockley-Queisser limit because it applies more broadly to essentially any possible solar power system: Click here.)
Video game prototype for teaching elementary circuit theory: Details here
2. Random blog posts
(Almost all of my blog posts are related to AGI, neuroscience, or both; those are listed on a different page. But sometimes I want to blog something random.)
• A couple productivity tips for overthinkers (Apr 2024)
• Some (problematic) aesthetics of what constitutes good work in academia (March 2024)
• Late-talking kid part 3: gestalt language learning (Oct 2023)
• My checklist for publishing a blog post (Aug 2023)
• My side of an argument with Jacob Cannell about chip interconnect losses (Jun 2023)
• More notes from raising a late-talking kid (Dec 2022)
• Changing the world through slack & hobbies (July 2022)
• Is Grabby Aliens built on good anthropic reasoning? (March 2022)
• Parenting: "Try harder next time" is bad advice for kids too (Dec 2021)
• Research productivity tip: "Solve The Whole Problem Day" (Aug 2021)
• Book review: Feeling Great by David Burns (June 2021)
• Electric heat pumps (Mini-Splits) vs Natural gas boilers (May 2021)
• Late-talking kids and "Einstein syndrome" (Feb 2021)
• Selling real estate: should you overprice or underprice? (July 2020)
3. Other things
My guide to touch-typing unicode special characters: Click here
If you’re a scientist, engineer, or mathematician, you probably frequently type technical things on a computer. If so, it's worth learning to touch-type critical characters that are not on your standard keyboard—characters like π μ Δ ± × ≈ β φ ° ∇ ∞ ∫ ≲ etc. etc., and this is my guide to doing that.
Notes on getting and recovering from Repetitive Strain Injury (RSI) in 2006-7:
Weird story. I have notes from the time here, and a much later (2022) blog post making sense of it at The “mind-body vicious cycle” model of RSI & back pain.
Physics GRE study sheet: Click here for PDF
A review-and-memorization sheet I made when preparing for the Physics GRE in college.
Fermi-level terminology guide: Click here
This is my guide to the confusing and inconsistent way that the terms “fermi level”, “fermi energy”, “electrochemical potential”, “chemical potential”, etc., are used in different fields of physics and chemistry.
4. Term papers, from when I was a student
Introduction to Schottky-Barrier and “MIS-IL” solar cells: PAPER and PRESENTATION
This paper gives an introduction and overview of Schottky-barrier solar cells (and their fancier cousins, MIS-IL solar cells). Researchers often make these types of solar cells when exploring new materials, but they are not produced commercially (as far as I know). Why not? I wrote this as a term paper for a solar cell physics course in grad school.
Polarons: Click here for PDF
This is a brief introduction to “polarons”, a concept in solid-state physics. I wrote this as a term paper for a semiconductor materials course in grad school.
Phonon pumping: Click here for PDF
This is a paper about whether you can make a laser from silicon (or other “indirect-bandgap” materials) by “phonon pumping”–i.e., trying to set up stimulated emission of phonons and photons simultaneously. (A normal laser is just photons.) I thought it was a great idea for a few days, but then discovered that it doesn’t work. (There are too many phonon modes!) I’m sure many other people have figured this out too. I wrote this as a term paper for an AMO (atomic, molecular, and optical) physics course in grad school.
Representation theory of S(N) and SU(N): Click here for PDF
This paper is a very basic introduction the representation theory of, first, the symmetric groups (aka permutation groups) and second, the family of Lie algebras which physicists call SU(N) and mathematicians call SL(N). I wrote this as a term paper for an abstract algebra course in college.
The number field sieve: Click here for PDF
This paper is a very basic introduction to the Number Field Sieve, a famous prime factorization algorithm. I wrote this as a term paper for an introductory abstract algebra course in college.
